4.1 INTRODUCTION

Digital filters with finite impulse response can be considered as part of the deterministic discrete linear systems, which are invariant in time. Their digital output, representing the samples of the filtered signal, comes from a weighted summation of a finite set of digital input data, which are the samples of the signal to be filtered.

The coefficients of the weighted summation constitute the impulse response of the filter, and just a finite number of them are different from zero.

These filters are considered to be with finite memory; that is, they give an output as a function of a limited number of inputs. They are also known as non-recursive because they don’t require a feedback loop in their implementation.

Although the infinite impulse response filters have very attractive properties, they also have some drawbacks. In fact, if from on side the IIR filters generally give excellent amplitude responses, from the other side they give a phase response that is not linear. At the contrary, the FIR filters can have phase response strictly linear.

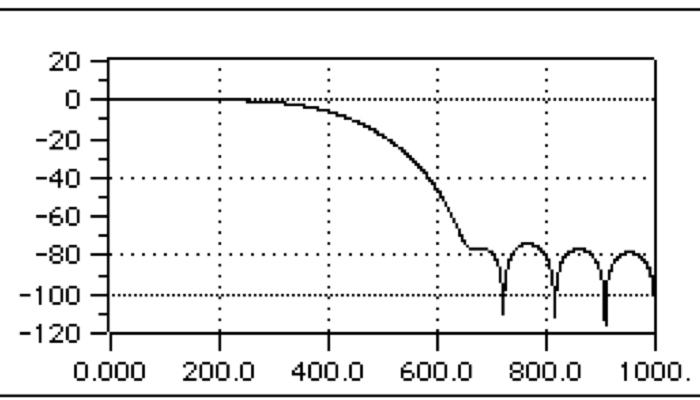
An immediate design method for a FIR filter is to obtain an impulse response with a finite length of time by truncating an infinite impulse response.

The approximation of the design specifications of an ideal filter by truncating an ideal impulse response leads to some problems (like the Gibbs effect). These problems can be highlighted from the study of the Fourier series convergence.

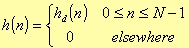
where hd(n) represents the infinite impulse response.

In other words, generally the finite impulse response of a FIR filter can be thought as the product of the infinite impulse response with a finite length of time window. This window, in the simple above expression, is of rectangular type.

To reduce the Gibbs effects, you can truncate the Fourier series in a less abruptly way. In other words, you can use windows different from the rectangular one.

It has been also demonstrated the main central lobe of the window Fourier transform is narrow in the frequency space. Then, the result from the convolution between the desired frequency response and the window Fourier transform, matches quite well the design specifications.

Hence, from one side, there is the need to have a window as short as possible in the time space (to reduce the computational complexity during the filtering processing,) and we need a window as narrow as possible in the frequency space (to produce with a higher accuracy as possible, the desired response,) on the other end. Of course, these two requirements are in contrast.

Moreover, the fact of having a longer or shorter time duration of the window does not affect the amplitude of the ripples due to the Gibbs effect. In fact, as in the case of a RECTANGULAR window (i.e. a simple abrupt truncation of the infinite impulse response,) the side lobes are not negligible. As the window number of points grows, the main lobe peak value, as well as the ones of the side lobes, becomes bigger so that the area underneath each lobe is constant, while the width of each lobe decreases as the number of points increase.

With this proviso, when the desired frequency response is a discontinuous function, the convolution between the desired frequency response and the window transform produces ripples while the lobes will result overlapped in the discontinuous point. As the number of the window points grows, the ripple amplitude does not decrease but simply grows.

It is well known from the Fourier series theory that this not uniform convergence can be reduced using a smoothly series truncation.

We can reduce the height of the secondary lobes letting the window do tend slowly to zero at its sides; this causes the main lobe to be broaden, and therefore a less steep decay in the discontinuous point.

next >

< previous